10 Método de Box-Muller
O objetivo desta aula é utilizar variáveis aleatórias uniformes para gerar valores de uma nova variável aleatória com uma distribuição de probabilidade específica. Nesta aula, focaremos na geração de variáveis aleatórias com distribuição Normal, usando o método de Box-Muller.
10.1 Representação em Coordenadas Polares
Considere duas variáveis aleatórias \(X \sim N(0, 1)\) e \(Y \sim N(0, 1)\), independentes entre si. No plano cartesiano, podemos representar o ponto \((X, Y)\) e explorar sua distribuição em coordenadas polares \((R, \Theta)\), onde \(R\) representa a distância do ponto à origem e \(\Theta\) é o ângulo formado com o eixo horizontal.
As relações trigonométricas para \(\Theta\) são dadas por:
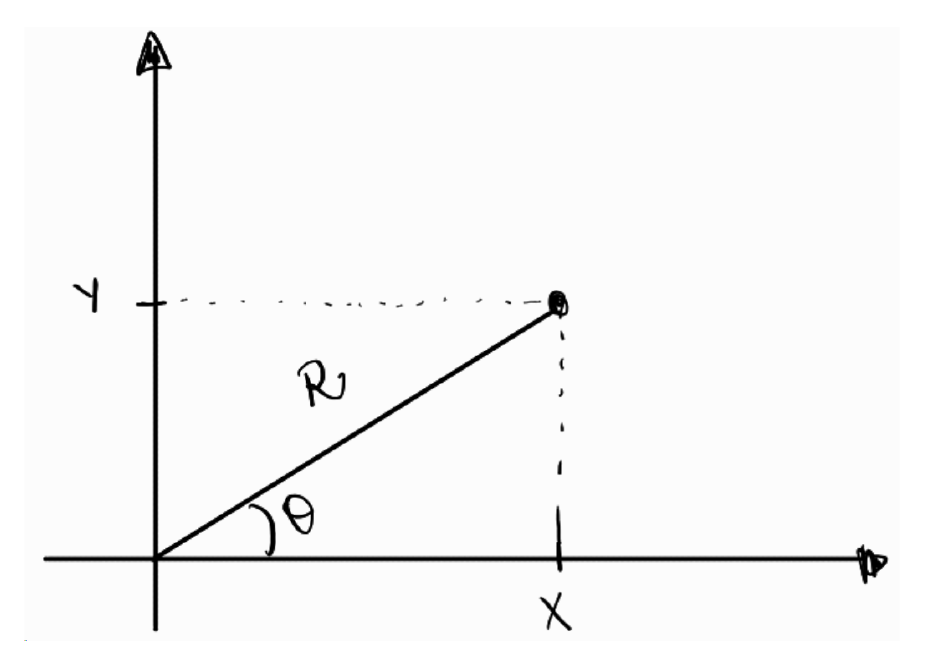
\[ \sin \Theta = \frac{\text{cateto oposto}}{\text{hipotenusa}} \]
\[ \cos \Theta = \frac{\text{cateto adjacente}}{\text{hipotenusa}} \]
Para \((X, Y)\) normalmente distribuído, queremos expressá-lo em coordenadas polares, de modo que:
\[ \sin \Theta = \frac{Y}{R} \]
\[ \cos \Theta = \frac{X}{R} \]
Dessa forma, obtemos:
\[ X = R \cos \Theta \quad \text{e} \quad Y = R \sin \Theta \]
Além disso, temos que:
\[ R^2 = X^2 + Y^2 \]
10.2 Transformação de Variáveis
As variáveis \(R\) e \(\Theta\) podem ser obtidas a partir de uma transformação das variáveis \((X, Y)\). A função de densidade conjunta de \((R, \Theta)\) é dada por:
\[ f_{R, \Theta}(r, \theta) = f_{X, Y}(h_1(r, \theta), h_2(r, \theta)) |J_h(r, \theta)| \]
onde \(J_h(r, \theta)\) é o Jacobiano referente às funções \(h_1\) e \(h_2\), sendo essas funções as transformações inversas que expressam \(X\) e \(Y\) em termos de \(R\) e \(\Theta\). Esse Jacobiano pode ser calculado pelo determinante:
\[ J_h(r, \theta) = \begin{vmatrix} \frac{\partial h_1}{\partial r} & \frac{\partial h_1}{\partial \theta} \\ \frac{\partial h_2}{\partial r} & \frac{\partial h_2}{\partial \theta} \\ \end{vmatrix} \]
Neste caso, o Jacobiano é dado por:
\[ J_h(r, \theta) = \begin{vmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \\ \end{vmatrix} = r(\cos^2 \theta + \sin^2 \theta) = r \]
Com o Jacobiano, a densidade conjunta é:
\[ f_{R, \Theta}(r, \theta) = f_{X, Y}(r \cos \theta, r \sin \theta) |J_h(r, \theta)| = \frac{1}{2\pi} e^{-\frac{1}{2}(r^2)} r, \] para \(0 < r < \infty, \, 0 < \theta < 2\pi\).
Assim, obtemos que:
\[ f_{\Theta}(\theta) = \frac{1}{2\pi}, \quad 0 < \theta < 2\pi \]
\[ f_R(r) = r e^{-r^2/2}, \quad 0 < r < \infty \]
Logo, \(\Theta \sim \text{Unif}(0, 2\pi)\) e \(R \sim \text{Rayleigh}(1)\), sendo \(R\) e \(\Theta\) independentes.
Além disso, sabe-se que se \(R \sim \text{Rayleigh}(1)\), então \(R^2 \sim \chi^2_2\) (exercício). Se \(R^2 \sim \chi^2_2\), então \(R^2 \sim \text{Exp}(1/2)\) (exercício). Portanto:
\[ \Theta \sim \text{Unif}(0, 2\pi) \quad \text{e} \quad R^2 \sim \text{Exp}(1/2) \]
10.3 Resumindo
Considerando \(X \sim N(0, 1)\) e \(Y \sim N(0, 1)\), variáveis independentes, podemos expressá-las em termos das coordenadas polares \((R, \Theta)\), onde:
\[ X = R \cos \Theta \quad \text{e} \quad Y = R \sin \Theta \]
Com essa transformação, obtemos que \(\Theta\) tem distribuição uniforme no intervalo \((0, 2\pi)\) e que \(R^2\) segue uma distribuição exponencial com parâmetro \(1/2\):
\[ \Theta \sim \text{Unif}(0, 2\pi) \quad \text{e} \quad R^2 \sim \text{Exp}(1/2) \]
Além disso, as variáveis \(R^2\) e \(\Theta\) são independentes.
10.4 Como Gerar \(R^2\) e \(\Theta\)
Para obter valores de \(R^2\) e \(\Theta\) de acordo com as distribuições acima, podemos seguir estes passos:
- Primeiramente, geramos duas variáveis uniformes independentes \(U_1 \sim \text{Unif}(0, 1)\) e \(U_2 \sim \text{Unif}(0, 1)\).
- Em seguida, calculamos \(R^2 = -2 \log U_1\) e \(\Theta = 2\pi U_2\).
Essa abordagem nos permite obter \(R^2\) e \(\Theta\) de acordo com as distribuições desejadas.
10.5 Simulação - Distribuição Normal
Para gerar duas variáveis independentes \(X\) e \(Y\), ambas com distribuição \(N(0, 1)\), utilizamos o método de Box-Muller. O procedimento é o seguinte:
- Primeiramente, geramos duas variáveis uniformes independentes \(U_1 \sim \text{Unif}(0, 1)\) e \(U_2 \sim \text{Unif}(0, 1)\).
- Em seguida, aplicamos as fórmulas \(X = \sqrt{-2 \log U_1} \cos(2\pi U_2)\) e \(Y = \sqrt{-2 \log U_1} \sin(2\pi U_2)\).
O método de Box-Muller permite que convertemos variáveis uniformes em variáveis com distribuição normal padrão, mantendo a independência entre \(X\) e \(Y\).
10.6 Exercícios
Exercício 1.
Implemente o método de Box-Muller para gerar duas variáveis aleatórias independentes com distribuição normal \(N(0, 1)\) a partir de variáveis uniformes \(U_1\) e \(U_2\).
Exercício 2.
Suponha \(X \sim N(0, 1)\). Encontre a transformação para obter \(X' \sim N(\mu, \sigma^2)\) e implemente um algorítmo que gera \(X' \sim N(\mu, \sigma^2)\).