8  Método da Rejeição para Variáveis Contínuas

A amostragem por rejeição é uma técnica útil para gerar variáveis aleatórias a partir de uma distribuição complexa, utilizando uma distribuição proposta mais simples. A ideia básica é simular de uma distribuição fácil de amostrar e, em seguida, rejeitar ou aceitar essas amostras com base na distribuição alvo.

8.1 Algoritmo

O método assume que conhecemos uma distribuição \(g(x)\), fácil de simular, que cubra o suporte da distribuição alvo \(f(x)\). Essa distribuição é chamada de distribuição proposta. Além disso ele assume que existe \(c\) tal que \(\frac{f(x)}{g(x)} \leq c\) para todo \(x\), e que conseguimos calcular \(c\). O método de aceitação e rejeição segue os seguintes passos:

  1. Gere um valor \(Y\) da distribuição proposta \(g(x)\).

  2. Gere um valor \(U \sim \text{Uniform}(0, 1)\).

  3. Aceite \(Y\) como uma amostra de \(f(x)\) se \(U \leq \frac{f(Y)}{c \cdot g(Y)}\), caso contrário, rejeite \(Y\) e repita o processo.

A figura a seguir ilustra esse processo quando \(g\) é uma distribuição uniforme entre 0 e 1.

Mostrar código 
library(ggplot2)

# Função densidade alvo f(x)
f <- function(x) {
  20 * x * (1 - x)^3
}

# Função densidade proposta g(x) (distribuição uniforme)
g <- function(x) {
  rep(1, length(x))  # g(x) é uniforme no intervalo (0, 1)
}

# Constante c (máximo de f(x))
opt_result <- optimize(f = function(x) -f(x), interval = c(0, 1))
c <- f(opt_result$minimum)

# Gerar valores de x
x <- seq(0, 1, length.out = 1000)

# Valor de Y para aceitar/rejeitar (escolhido aleatoriamente)
Y <- 0.6

# DataFrame para o gráfico
df <- data.frame(x = x, fx = f(x), gx = c * g(x))

# Plotando as funções f(x) e a linha horizontal c*g(x)
ggplot(df, aes(x = x)) +
  geom_line(aes(y = fx, color = "f(x)"), size = 1) +
  geom_hline(aes(yintercept = c * g(x), color = "c * g(x)"), size = 1.5) +
  
  # Destacar a área de aceitação e rejeição
  geom_text(aes(x = Y + 0.025, y = 0.05, label = "Y"), color = "black", size = 5) +
  
  geom_segment(aes(x = Y, xend = Y, y = 0, yend = f(Y)), color = "green", size = 1.5) +
  geom_segment(aes(x = Y, xend = Y, y = f(Y), yend = c * g(Y)), color = "red", size = 1.5) +
  
  # Mover rótulos de Aceitar/Rejeitar para a esquerda da linha Y
  geom_text(aes(x = Y + 0.06, y = f(Y) / 2, label = "Aceitar x"), color = "green", size = 4) +
  geom_text(aes(x = Y + 0.06, y = f(Y) + (c * g(Y) - f(Y)) / 2, label = "Rejeitar x"), color = "red", size = 4) +
  
  # Limites e rótulos
  xlim(0, 1) +
  ylim(0, 2.5) +
  labs(x = "x", y = "Densidade", title = "Amostragem por Rejeição para g uniforme") +
  
  # Legenda
  scale_color_manual(values = c("f(x)" = "black", "c * g(x)" = "blue"), name = "Funções") +
  
  theme_minimal() +
  theme(legend.position = "top")

Mostrar código 
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar

# Função densidade alvo f(x)
def f(x):
    return 20 * x * (1 - x)**3

# Função densidade proposta g(x) (distribuição uniforme)
def g(x):
    return 1  # g(x) é uniforme no intervalo (0, 1)

# Constante c
result = minimize_scalar(lambda x: -f(x), bounds=(0, 1), method='bounded')
c = f(result.x)

# Gerar valores de x
x = np.linspace(0, 1, 1000)

# Valor de Y para aceitar/rejeitar (escolhido aleatoriamente)
Y = 0.6
U = 0.8
accept_threshold = f(Y) / (c * g(Y))

# Plotando as funções f(x) e a linha horizontal c*g(x)
# Ajustando o código para truncar o eixo y no zero
plt.plot(x, f(x), label='f(x)', color='black')
plt.hlines(c * g(x), 0, 1, color='blue', label='c*g(x)', linewidth=2)  # Linha horizontal c*g(x)

# Destacar a área de aceitação e rejeição
plt.vlines(Y, 0, f(Y), colors='green', label='Aceitar $x$', linewidth=2)
plt.vlines(Y, f(Y), c * g(Y), colors='red', label='Rejeitar $x$', linewidth=2)

# Adicionar rótulo de Y na posição da linha vertical
plt.text(Y+0.025, 0.05, 'Y', color='black', fontsize=12, horizontalalignment='center')

# Adicionar rótulos de Aceitar/Rejeitar
plt.text(Y + 0.01, f(Y) / 2, 'Aceitar x', color='green', fontsize=10, verticalalignment='center')
plt.text(Y + 0.01, f(Y) + (c * g(Y) - f(Y)) / 2, 'Rejeitar x', color='red', fontsize=10, verticalalignment='center')

# Limites e rótulos
plt.xlim(0, 1)
(0.0, 1.0)
Mostrar código 
plt.ylim(0, 2.5)  # Truncando o eixo y no zero
(0.0, 2.5)
Mostrar código 
plt.xlabel('x')
plt.ylabel('Densidade')

# Adicionar a legenda para f(x) e c*g(x)
plt.legend(['f(x)', 'c*g(x)'])

# Mostrar gráfico
plt.title('Amostragem por Rejeição para g uniforme')
plt.show()

8.2 Exemplo

Vamos demonstrar a amostragem por rejeição gerando amostras de uma distribuição alvo \(f(x)\), utilizando a distribuição uniforme como distribuição proposta.

A função densidade alvo que utilizaremos é: \[ f(x) = 20x(1 - x)^3 \quad \text{para} \quad 0 < x < 1 \] E a distribuição proposta será \(g(x) = 1 \quad \text{para} \quad 0 < x < 1\), que é uma distribuição uniforme.

Implementamos o seguinte algoritmo:

Mostrar código 
library(ggplot2)

# Função densidade alvo f(x)
f <- function(x) {
  20 * x * (1 - x)^3
}

# Amostragem por rejeição
amostragem_rejeicao <- function(f, c, n_amostras) {
  amostras <- numeric(0)
  while (length(amostras) < n_amostras) {
    # Gere Y ~ g(x) (uniforme entre 0 e 1)
    Y <- runif(1, 0, 1)
    
    # Gere U ~ Uniforme(0, 1)
    U <- runif(1, 0, 1)
    
    # Verifica se aceitamos Y
    if (U <= f(Y) / (c)) {
      amostras <- c(amostras, Y)
    }
  }
  return(amostras)
}

# A constante c é o limite superior de f(x)
c <- 135 / 64

# Gere 1000 amostras usando o método de aceitação e rejeição
set.seed(123)
amostras <- amostragem_rejeicao(f, c, 1000)

# Criação do data frame para o ggplot2
x_vals <- seq(0, 1, length.out = 1000)
f_vals <- f(x_vals)
df <- data.frame(x = x_vals, y = f_vals)

# Gráfico com ggplot2
ggplot() +
  geom_line(data = df, aes(x = x, y = y), color = 'blue', size = 1, linetype = 'solid') +
  geom_histogram(aes(x = amostras, y = ..density..), bins = 30, fill = 'orange', alpha = 0.5, color = 'black') +
  ggtitle("Amostragem por Rejeição") +
  xlab("x") +
  ylab("Densidade") +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))

Mostrar código 
import numpy as np
import matplotlib.pyplot as plt

# Função densidade alvo f(x)
def f(x):
    return 20 * x * (1 - x)**3

# Função densidade proposta g(x) (distribuição uniforme)
def g(x):
    return 1  # g(x) é uniforme no intervalo (0, 1)

# Amostragem por rejeição
def amostragem_rejeicao(f, g, c, n_amostras):
    amostras = []
    while len(amostras) < n_amostras:
        # Gere Y ~ g(x)
        Y = np.random.uniform(0, 1)
        
        # Gere U ~ Uniforme(0, 1)
        U = np.random.uniform(0, 1)
        
        # Verifica se aceitamos Y
        if U <= f(Y) / (c * g(Y)):
            amostras.append(Y)
     
    return np.array(amostras)
 
# A constante c é o limite superior de f(x)/g(x)
c = 135 / 64  # Pré-calculado

# Gere 1000 amostras usando o método de aceitação e rejeição
amostras = amostragem_rejeicao(f, g, c, 1000)

# Plotando os resultados
x = np.linspace(0, 1, 1000)
plt.plot(x, f(x), label='Distribuição Alvo f(x)')
plt.hist(amostras, bins=30, density=True, alpha=0.5, label='Amostragem por Rejeição')
plt.legend()
plt.title("Amostragem por Rejeição")
plt.show()

8.3 Resultados Teóricos

8.3.1 Correção do Método de Aceitação e Rejeição

Teorema:
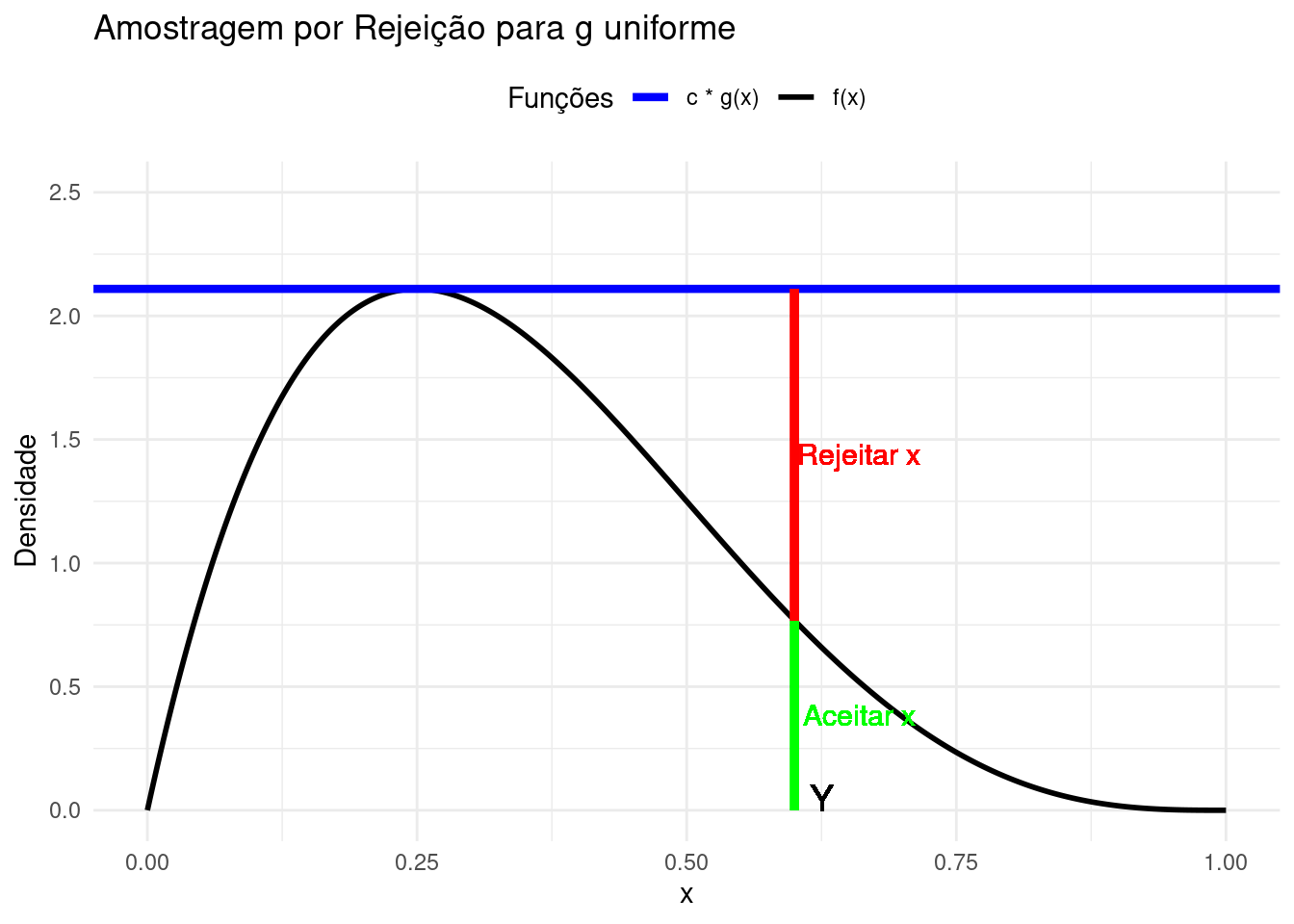
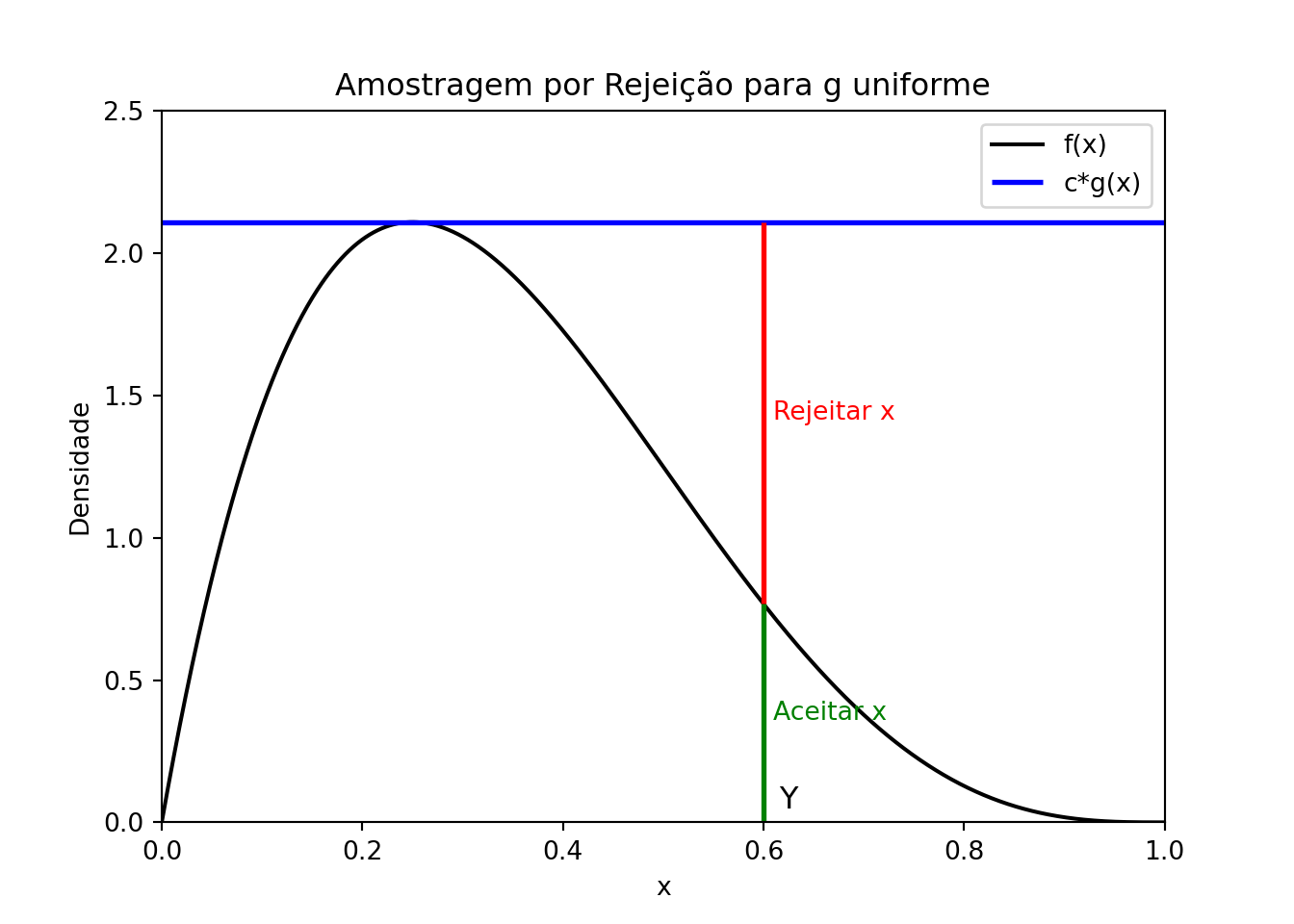
A variável aleatória \(Y\) gerada pelo método da rejeição tem densidade \(f(x)\).

Prova:

Considere a função de distribuição acumulada (CDF) de \(X\), a variável gerada pelo método:

\[ P(X \leq x) = P(Y \leq x \mid \text{aceitar } Y) \]

Podemos escrever essa probabilidade como:

\[ P(X \leq x) = \frac{P(Y \leq x, U \leq \frac{f(Y)}{c \cdot g(Y)})}{P(U \leq \frac{f(Y)}{c \cdot g(Y)})} \]

Usando a probabilidade condicional, o numerador pode ser expresso como:

\[ P(Y \leq x, U \leq \frac{f(Y)}{c \cdot g(Y)}) = \int_{-\infty}^x \int_0^{\frac{f(y)}{c \cdot g(y)}} g(y) \, du \, dy \]

Resolvendo a integral em \(u\):

\[ P(Y \leq x, U \leq \frac{f(Y)}{c \cdot g(Y)}) = \int_{-\infty}^x \frac{f(y)}{c \cdot g(y)} g(y) \, dy = \frac{1}{c} \int_{-\infty}^x f(y) \, dy \]

De maneira semelhante, o denominador é dado por:

\[ P\left(U \leq \frac{f(Y)}{c \cdot g(Y)}\right) = \int_{-\infty}^{\infty} \frac{f(y)}{c \cdot g(y)} g(y) \, dy = \frac{1}{c} \int_{-\infty}^{\infty} f(y) \, dy \]

Como \(\int_{-\infty}^{\infty} f(y) \, dy = 1\) (pois \(f(x)\) é uma função densidade), o denominador resulta em \(\frac{1}{c}\). Substituindo essas expressões na equação original, obtemos:

\[ P(X \leq x) = \frac{\frac{1}{c} \int_{-\infty}^x f(y) \, dy}{\frac{1}{c}} = \int_{-\infty}^x f(y) \, dy \]

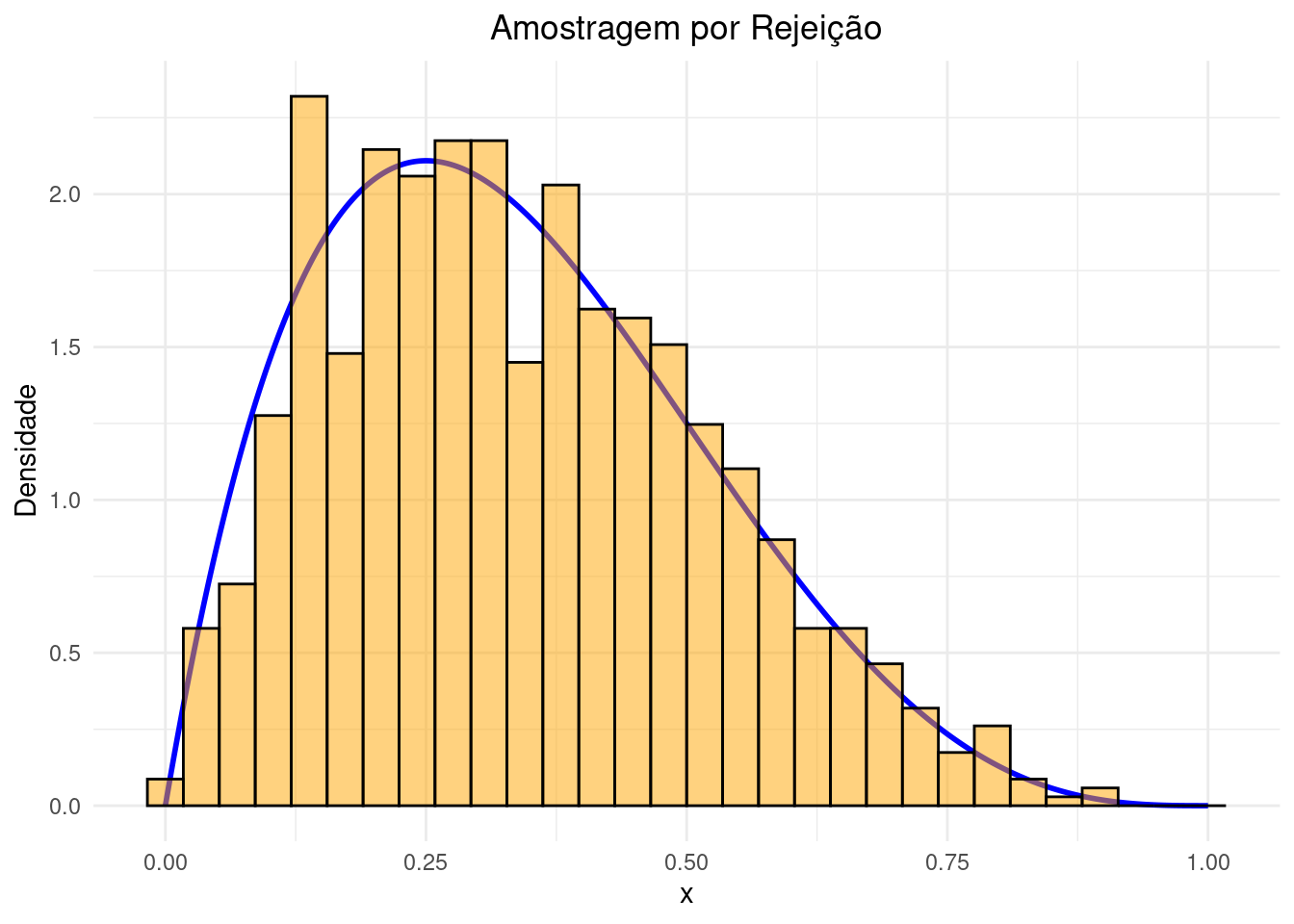
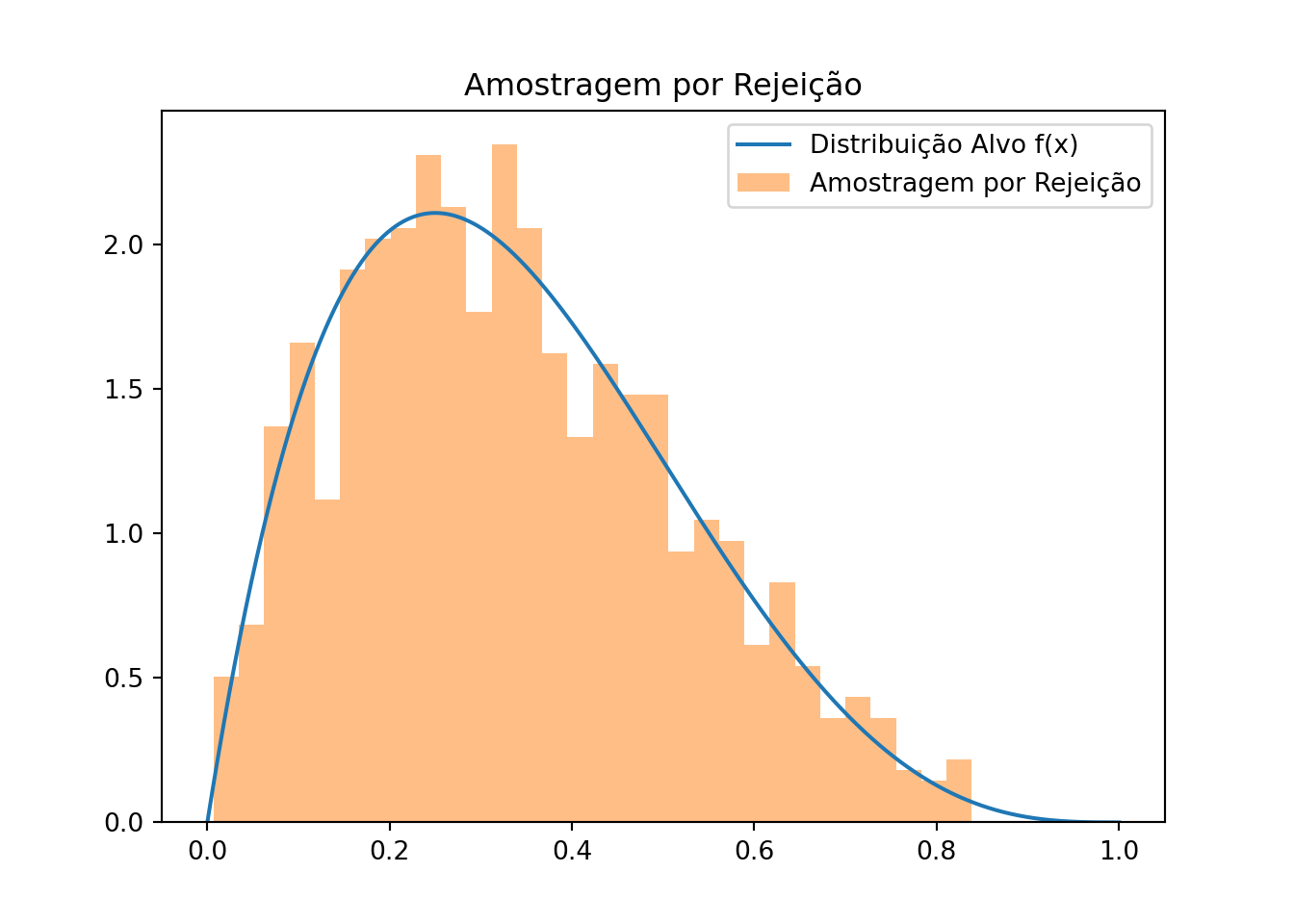
Portanto, a variável \(X\) gerada pelo método de aceitação e rejeição tem função de distribuição acumulada \(\int_{-\infty}^x f(y) \, dy\), o que implica que \(X\) tem densidade \(f(x)\). Assim, o método gera amostras corretamente distribuídas de acordo com \(f(x)\), como desejado.

8.3.2 Eficiência computacional

Teorema:

A variável aleatória gerada pelo método de aceitação e rejeição tem função de densidade \(f(x)\). O número de passos que o algoritmo necessita para gerar \(X\) tem distribuição geométrica com média \(c\), onde \(c\) é a constante de normalização que define o limite superior da razão \(\frac{f(x)}{g(x)}\).

Prova:

Seja \(Y\) a variável aleatória gerada pela distribuição proposta \(g(x)\), e \(U \sim \text{Unif}(0, 1)\) uma variável aleatória uniforme. O método de aceitação e rejeição aceita \(Y\) como amostra de \(f(x)\) se \(U \leq \frac{f(Y)}{c g(Y)}\), caso contrário, o valor é rejeitado e o processo é repetido.

A probabilidade de aceitar uma amostra \(Y\), dado que \(Y \leq x\), é dada por:

\[ P(Y \leq x \text{ e aceitar}) = P\left(Y \leq x , U \leq \frac{f(Y)}{c g(Y)}\right) \]

Podemos reescrever essa probabilidade como uma integral:

\[ P(Y \leq x \text{ e aceitar}) = \int_{-\infty}^x \int_{0}^{\frac{f(y)}{c g(y)}} g(y) \, du \, dy \]

Resolvendo a integral em \(u\), temos:

\[ P(Y \leq x \text{ e aceitar}) = \int_{-\infty}^x \frac{f(y)}{c g(y)} g(y) \, dy = \frac{1}{c} \int_{-\infty}^x f(y) \, dy \]

A probabilidade de aceitar qualquer valor \(Y\) é dada por:

\[ P(\text{aceitar}) = P\left(U \leq \frac{f(Y)}{c g(Y)}\right) = \int_{-\infty}^{\infty} \int_{0}^{\frac{f(y)}{c g(y)}} g(y) \, du \, dy \]

Simplificando:

\[ P(\text{aceitar}) = \int_{-\infty}^{\infty} \frac{f(y)}{c g(y)} g(y) \, dy = \frac{1}{c} \int_{-\infty}^{\infty} f(y) \, dy = \frac{1}{c} \]

Assim, a cada passo, a probabilidade de aceitar um valor é \(\frac{1}{c}\), o que implica que o número de passos necessários para aceitar uma amostra tem distribuição geométrica com média \(c\).

Por fim, sabemos que a função de distribuição acumulada da variável \(X\), dado que ela foi aceita, é:

\[ P(X \leq x) = P(Y \leq x \mid \text{aceitou}) = \frac{P(Y \leq x , \text{aceitou})}{P(\text{aceitar})} \]

Substituindo as expressões:

\[ P(X \leq x) = \frac{\frac{1}{c} \int_{-\infty}^x f(y) \, dy}{\frac{1}{c}} = \int_{-\infty}^x f(y) \, dy \]

Portanto, a variável \(X\) gerada pelo método de aceitação e rejeição tem função de densidade \(f(x)\), como desejado.

8.4 Exercícios

Exercício 1. Seja \(X\sim Gama(3/2,1)\) com função densidade dada por \[f(x)=\frac{1}{\Gamma(3/2)}x^{1/2}e^{-x}, \text{ para } x > 0.\]

  1. Escreva um pseudo-algoritmo para simular um valor da distribuição de \(X\) usando o método da aceitação e rejeição usando como distribuição proposta a distribuição exponencial de parâmetro \(2/3\).

Observação: Note que \(\mathbb E[X]=3/2\) e \(\mathbb E[Y]=3/2\), por isso o parâmetro da distribuição exponencial proposta foi tomado como \(2/3\).

  1. Crie uma função para gerar um valor de \(X\).

  2. Qual foi o número de passos necessários para gerar um valor de \(X\)? Compare com o valor real.

  3. Crie uma função para gerar uma amostra de tamanho \(n\) de \(X\).

  4. Qual foi o número médio de passos necessários para gerar a amostra de tamanho \(n\)?

  5. Compare a distribuição empírica dos valores simulados com a distribuição real de \(X\).